A Synergistic Multi-Layered Approach for Falsification of Specifications for Hybrid Systems
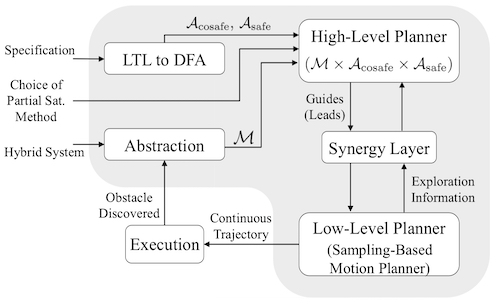
Hybrid systems, which combine discrete and continuous dynamics, provide sophisticated mathematical models for automated highway systems, air traffic control, biological systems, and other applications. A key feature of such systems is that they are often deployed in safety-critical scenarios and hence designing such systems with provable guarantees is very important. This is usually done through analysis of such systems with regard to a given set of safety properties that assert that nothing 'bad' happens during the operation of the system. As more complex hybrid systems are considered, limiting safety properties to a set of unsafe states, as in current methods, considerably restricts the ability of designers to adequately express the desired safe behavior of the system. To allow for more sophisticated properties, researchers have advocated the use of linear temporal logic (LTL), which makes it possible to express temporal safety properties. This project develops algorithmic tools for safety analysis of embedded and hybrid systems operating under the effect of exogenous inputs and for LTL specifications. The problem addressed is the following: Given a hybrid system and a safety specification described using LTL, can a feasible trajectory be constructed for the system that violates the specification, when such a trajectory exists? The problem is called the falsification problem. The broader impact of the project is implemented through course development, involvement in research activities of undergraduate, graduate and postdoctoral students, efforts to mentor underrepresented groups, and dissemination of concepts through educational software developed at Rice.
This work has been supported by grant NSF SHF 1018798.
Related Publications
- M. Lahijanian, M. R. Maly, D. Fried, L. E. Kavraki, H. Kress-Gazit, and M. Y. Vardi, “Iterative Temporal Planning in Uncertain Environments with Partial Satisfaction
Guarantees,” IEEE Transactions on Robotics, vol. 32, no. 3, pp. 583–599, 2016.
BibTeX
@article{lahijanian2016iterative, title = {Iterative Temporal Planning in Uncertain Environments with Partial Satisfaction Guarantees}, author = {Lahijanian, Morteza and Maly, Matthew R. and Fried, Dror and Kavraki, Lydia E. and Kress-Gazit, Hadas and Vardi, Moshe Y.}, journal = {IEEE Transactions on Robotics}, year = {2016}, volume = {32}, number = {3}, pages = {583--599}, doi = {10.1109/TRO.2016.2544339}, abstract = {This work introduces a motion-planning framework for a hybrid system with general continuous dynamics to satisfy a temporal logic specification consisting of co-safety and safety components in a partially unknown environment. The framework employs a multi-layered synergistic planner to generate trajectories that satisfy the specification and adopts an iterative replanning strategy to deal with unknown obstacles. When the discovery of an obstacle renders the specification unsatisfiable, a division between the constraints in the specification is considered. The co-safety component of the specification is treated as a soft constraint, whose partial satisfaction is allowed, while the safety component is viewed as a hard constraint, whose violation is forbidden. To partially satisfy the co-safety component, inspirations are taken from indoor-robotic scenarios, and three types of (unexpressed) restrictions on the ordering of sub-tasks in the specification are considered. For each type, a partial satisfaction method is introduced, which guarantees the generation of trajectories that do not violate the safety constraints while attending to partially satisfying the co-safety requirements with respect to the chosen restriction type. The efficacy of the framework is illustrated through case studies on a hybrid car-like robot in an office environment.}, keyword = {planning from high-level specifications} }DetailsAbstract
This work introduces a motion-planning framework for a hybrid system with general continuous dynamics to satisfy a temporal logic specification consisting of co-safety and safety components in a partially unknown environment. The framework employs a multi-layered synergistic planner to generate trajectories that satisfy the specification and adopts an iterative replanning strategy to deal with unknown obstacles. When the discovery of an obstacle renders the specification unsatisfiable, a division between the constraints in the specification is considered. The co-safety component of the specification is treated as a soft constraint, whose partial satisfaction is allowed, while the safety component is viewed as a hard constraint, whose violation is forbidden. To partially satisfy the co-safety component, inspirations are taken from indoor-robotic scenarios, and three types of (unexpressed) restrictions on the ordering of sub-tasks in the specification are considered. For each type, a partial satisfaction method is introduced, which guarantees the generation of trajectories that do not violate the safety constraints while attending to partially satisfying the co-safety requirements with respect to the chosen restriction type. The efficacy of the framework is illustrated through case studies on a hybrid car-like robot in an office environment. - K. He, M. Lahijanian, L. E. Kavraki, and M. Y. Vardi, “Towards Manipulation Planning with Temporal Logic Specifications,” in Proceedings of the 2015 IEEE International Conference on Robotics and Automation
(ICRA), Seattle, WA, 2015, pp. 346–352.
BibTeX
@inproceedings{he-lahijanian2015towards-manipulation-planning, title = {Towards Manipulation Planning with Temporal Logic Specifications}, author = {He, Keliang and Lahijanian, Morteza and Kavraki, Lydia E. and Vardi, Moshe Y.}, booktitle = {Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA)}, month = may, year = {2015}, pages = {346--352}, doi = {10.1109/ICRA.2015.7139022}, abstract = {Manipulation planning from high-level task specifications, even though highly desirable, is a challenging problem. The large dimensionality of manipulators and complexity of task specifications make the problem computationally intractable. This work introduces a manipulation planning framework with linear temporal logic (LTL) specifications. The use of LTL as the specification language allows the expression of rich and complex manipulation tasks. The framework deals with the state-explosion problem through a novel abstraction technique. Given a robotic system, a workspace consisting of obstacles, manipulable objects, and locations of interest, and a co-safe LTL specification over the objects and locations, the framework computes a motion plan to achieve the task through a synergistic multi-layered planning architecture. The power of the framework is demonstrated through case studies, in which the planner efficiently computes plans for complex tasks. The case studies also illustrate the ability of the framework in intelligently moving away objects that block desired executions without requiring backtracking.}, address = {Seattle, WA}, keyword = {planning from high-level specifications}, publisher = {IEEE} }DetailsAbstract
Manipulation planning from high-level task specifications, even though highly desirable, is a challenging problem. The large dimensionality of manipulators and complexity of task specifications make the problem computationally intractable. This work introduces a manipulation planning framework with linear temporal logic (LTL) specifications. The use of LTL as the specification language allows the expression of rich and complex manipulation tasks. The framework deals with the state-explosion problem through a novel abstraction technique. Given a robotic system, a workspace consisting of obstacles, manipulable objects, and locations of interest, and a co-safe LTL specification over the objects and locations, the framework computes a motion plan to achieve the task through a synergistic multi-layered planning architecture. The power of the framework is demonstrated through case studies, in which the planner efficiently computes plans for complex tasks. The case studies also illustrate the ability of the framework in intelligently moving away objects that block desired executions without requiring backtracking. - M. Lahijanian, S. Almagor, D. Fried, L. E. Kavraki, and M. Y. Vardi, “This Time the Robot Settles for a Cost: A Quantitative Approach to Temporal Logic
Planning with Partial Satisfaction,” in Proceedings of The Twenty-Ninth AAAI Conference (AAAI-15), Austin, TX, 2015, pp. 3664–3671.
BibTeX
@inproceedings{lahijanian-almagor2015this-time-robot, title = {This Time the Robot Settles for a Cost: A Quantitative Approach to Temporal Logic Planning with Partial Satisfaction}, author = {Lahijanian, Morteza and Almagor, Shaull and Fried, Dror and Kavraki, Lydia E and Vardi, Moshe Y.}, booktitle = {Proceedings of The Twenty-Ninth AAAI Conference (AAAI-15)}, month = jan, year = {2015}, pages = {3664--3671}, abstract = {The specification of complex motion goals through temporal logics is increasingly favored in robotics to narrow the gap between task and motion planning. A major limiting factor of such logics, however, is their Boolean satisfaction condition. To relax this limitation, we introduce a method for quantifying the satisfaction of co-safe linear temporal logic specifications, and propose a planner that uses this method to synthesize robot trajectories with the optimal satisfaction value. The method assigns costs to violations of specifications from user-defined proposition costs. These violation costs define a distance to satisfaction and can be computed algorithmically using a weighted automaton. The planner utilizes this automaton and an abstraction of the robotic system to construct a product graph that captures all possible robot trajectories and their distances to satisfaction. Then, a plan with the minimum distance to satisfaction is generated by employing this graph as the high-level planner in a synergistic planning framework. The efficacy of the method is illustrated on a robot with unsatisfiable specifications in an office environment.}, address = {Austin, TX}, keyword = {uncertainty}, publisher = {AAAI}, url = {http://www.aaai.org/ocs/index.php/AAAI/AAAI15/paper/view/10001} }DetailsAbstract
The specification of complex motion goals through temporal logics is increasingly favored in robotics to narrow the gap between task and motion planning. A major limiting factor of such logics, however, is their Boolean satisfaction condition. To relax this limitation, we introduce a method for quantifying the satisfaction of co-safe linear temporal logic specifications, and propose a planner that uses this method to synthesize robot trajectories with the optimal satisfaction value. The method assigns costs to violations of specifications from user-defined proposition costs. These violation costs define a distance to satisfaction and can be computed algorithmically using a weighted automaton. The planner utilizes this automaton and an abstraction of the robotic system to construct a product graph that captures all possible robot trajectories and their distances to satisfaction. Then, a plan with the minimum distance to satisfaction is generated by employing this graph as the high-level planner in a synergistic planning framework. The efficacy of the method is illustrated on a robot with unsatisfiable specifications in an office environment. - R. Luna, M. Lahijanian, M. Moll, and L. E. Kavraki, “Asymptotically Optimal Stochastic Motion Planning with Temporal Goals,” in Algorithmic Foundations of Robotics XI, Cham, 2015, pp. 335–352. Appeared at Workshop on the Algorithmic Foundations of Robotics (WAFR) 2014.
BibTeX
@inproceedings{luna-lahijanian2014asymptotically-optimal-stochastic, title = {Asymptotically Optimal Stochastic Motion Planning with Temporal Goals}, author = {Luna, Ryan and Lahijanian, Morteza and Moll, Mark and Kavraki, Lydia E}, note = {Appeared at Workshop on the Algorithmic Foundations of Robotics (WAFR) 2014.}, booktitle = {Algorithmic Foundations of Robotics XI}, year = {2015}, doi = {10.1007/978-3-319-16595-0_20}, abstract = {This work presents a planning framework that allows a robot with stochastic action uncertainty to achieve a high-level task given in the form of a temporal logic formula. The objective is to quickly compute a feedback control policy to satisfy the task specification with maximum probability. A top-down framework is proposed that abstracts the motion of a continuous stochastic system to a discrete, bounded- parameter Markov decision process (bmdp), and then computes a control policy over the product of the bmdp abstraction and a dfa representing the temporal logic specification. Analysis of the framework reveals that as the resolution of the bmdp abstraction becomes finer, the policy obtained converges to optimal. Simulations show that high-quality policies to satisfy complex temporal logic specifications can be obtained in seconds, orders of magnitude faster than existing methods.}, address = {Cham}, keyword = {uncertainty}, pages = {335--352}, isbn = {978-3-319-16595-0}, publisher = {Springer International Publishing} }DetailsAbstract
This work presents a planning framework that allows a robot with stochastic action uncertainty to achieve a high-level task given in the form of a temporal logic formula. The objective is to quickly compute a feedback control policy to satisfy the task specification with maximum probability. A top-down framework is proposed that abstracts the motion of a continuous stochastic system to a discrete, bounded- parameter Markov decision process (bmdp), and then computes a control policy over the product of the bmdp abstraction and a dfa representing the temporal logic specification. Analysis of the framework reveals that as the resolution of the bmdp abstraction becomes finer, the policy obtained converges to optimal. Simulations show that high-quality policies to satisfy complex temporal logic specifications can be obtained in seconds, orders of magnitude faster than existing methods. - R. Luna, M. Lahijanian, M. Moll, and L. E. Kavraki, “Optimal and Efficient Stochastic Motion Planning in Partially-Known Environments,” in Proceedings of The Twenty-Eighth AAAI Conference on Artificial Intelligence, Quebec City, Canada, 2014, pp. 2549–2555.
BibTeX
@inproceedings{luna-lahijanian2014optimal-and-efficient, title = {Optimal and Efficient Stochastic Motion Planning in Partially-Known Environments}, author = {Luna, Ryan and Lahijanian, Morteza and Moll, Mark and Kavraki, Lydia E}, booktitle = {Proceedings of The Twenty-Eighth AAAI Conference on Artificial Intelligence}, month = jul, year = {2014}, pages = {2549--2555}, abstract = {A framework capable of computing optimal control policies for a continuous system in the presence of both action and environment uncertainty is presented in this work. The framework decomposes the planning problem into two stages: an offline phase that reasons only over action uncertainty and an online phase that quickly reacts to the uncertain environment. Offline, a bounded-parameter Markov decision process (BMDP) is employed to model the evolution of the stochastic system over a discretization of the environment. Online, an optimal control policy over the BMDP is computed. Upon the discovery of an unknown environment feature during policy execution, the BMDP is updated and the optimal control policy is efficiently recomputed. Depending on the desired quality of the control policy, a suite of methods is presented to incorporate new information into the BMDP with varying degrees of detail online. Experiments confirm that the framework recomputes high-quality policies in seconds and is orders of magnitude faster than existing methods.}, address = {Quebec City, Canada}, keyword = {uncertainty}, url = {http://www.aaai.org/ocs/index.php/AAAI/AAAI14/paper/view/8457} }DetailsAbstract
A framework capable of computing optimal control policies for a continuous system in the presence of both action and environment uncertainty is presented in this work. The framework decomposes the planning problem into two stages: an offline phase that reasons only over action uncertainty and an online phase that quickly reacts to the uncertain environment. Offline, a bounded-parameter Markov decision process (BMDP) is employed to model the evolution of the stochastic system over a discretization of the environment. Online, an optimal control policy over the BMDP is computed. Upon the discovery of an unknown environment feature during policy execution, the BMDP is updated and the optimal control policy is efficiently recomputed. Depending on the desired quality of the control policy, a suite of methods is presented to incorporate new information into the BMDP with varying degrees of detail online. Experiments confirm that the framework recomputes high-quality policies in seconds and is orders of magnitude faster than existing methods. - R. Luna, M. Lahijanian, M. Moll, and L. E. Kavraki, “Fast Stochastic Motion Planning with Optimality Guarantees using Local Policy
Reconfiguration,” in Proceedings of the IEEE International Conference on Robotics and Automation, Hong Kong, China, 2014, pp. 3013–3019.
BibTeX
@inproceedings{luna-lahijanian2014fast-stochastic-motion, title = {Fast Stochastic Motion Planning with Optimality Guarantees using Local Policy Reconfiguration}, author = {Luna, Ryan and Lahijanian, Morteza and Moll, Mark and Kavraki, Lydia E}, booktitle = {Proceedings of the IEEE International Conference on Robotics and Automation}, month = may, year = {2014}, pages = {3013--3019}, doi = {10.1109/ICRA.2014.6907293}, abstract = {This work presents a framework for fast reconfiguration of local control policies for a stochastic system to satisfy a high-level task specification. The motion of the system is abstracted to a class of uncertain Markov models known as bounded-parameter Markov decision processes (BMDPs). During the abstraction, an efficient sampling-based method for stochastic optimal control is used to construct several policies within a discrete region of the state space in order for the system to transit between neighboring regions. A BMDP is then used to find an optimal strategy over the local policies by maximizing a continuous reward function; a new policy can be computed quickly if the reward function changes. The efficacy of the framework is demonstrated using a sequence of online tasks, showing that highly desirable policies can be obtained by reconfiguring existing local policies in just a few seconds.}, address = {Hong Kong, China}, keyword = {uncertainty} }DetailsAbstract
This work presents a framework for fast reconfiguration of local control policies for a stochastic system to satisfy a high-level task specification. The motion of the system is abstracted to a class of uncertain Markov models known as bounded-parameter Markov decision processes (BMDPs). During the abstraction, an efficient sampling-based method for stochastic optimal control is used to construct several policies within a discrete region of the state space in order for the system to transit between neighboring regions. A BMDP is then used to find an optimal strategy over the local policies by maximizing a continuous reward function; a new policy can be computed quickly if the reward function changes. The efficacy of the framework is demonstrated using a sequence of online tasks, showing that highly desirable policies can be obtained by reconfiguring existing local policies in just a few seconds. - M. Lahijanian, L. E. Kavraki, and M. Y. Vardi, “A Sampling-Based Strategy Planner for Nondeterministic Hybrid Systems,” in Proceedings of the International Conference on Robotics and Automation, Hong Kong, China, 2014, pp. 3005–3012.
BibTeX
@inproceedings{lahijanian-kavraki2014sampling-based-strategy-planner, title = {A Sampling-Based Strategy Planner for Nondeterministic Hybrid Systems}, author = {Lahijanian, Morteza and Kavraki, Lydia E and Vardi, Moshe Y.}, booktitle = {Proceedings of the International Conference on Robotics and Automation}, month = may, year = {2014}, pages = {3005--3012}, doi = {10.1109/ICRA.2014.6907292}, abstract = {This paper introduces a strategy planner for nondeterministic hybrid systems with complex continuous dynamics. The planner uses sampling-based techniques and game-theoretic approaches to generate a series of plans and decision choices that increase the chances of success within a fixed time budget. The planning algorithm consists of two phases: exploration and strategy improvement. During the exploration phase, a search tree is grown in the hybrid state space by sampling state and control spaces for a fixed amount of time. An initial strategy is then computed over the search tree using a game-theoretic approach. To mitigate the effects of nondeterminism in the initial strategy, the strategy improvement phase extends new tree branches to the goal, using the data that is collected in the first phase. The efficacy of this planner is demonstrated on simulation of two hybrid and nondeterministic car-like robots in various environments. The results show significant increases in the likelihood of success for the strategies computed by the two-phase algorithm over a simple exploration planner.}, address = {Hong Kong, China}, keyword = {uncertainty}, publisher = {IEEE} }DetailsAbstract
This paper introduces a strategy planner for nondeterministic hybrid systems with complex continuous dynamics. The planner uses sampling-based techniques and game-theoretic approaches to generate a series of plans and decision choices that increase the chances of success within a fixed time budget. The planning algorithm consists of two phases: exploration and strategy improvement. During the exploration phase, a search tree is grown in the hybrid state space by sampling state and control spaces for a fixed amount of time. An initial strategy is then computed over the search tree using a game-theoretic approach. To mitigate the effects of nondeterminism in the initial strategy, the strategy improvement phase extends new tree branches to the goal, using the data that is collected in the first phase. The efficacy of this planner is demonstrated on simulation of two hybrid and nondeterministic car-like robots in various environments. The results show significant increases in the likelihood of success for the strategies computed by the two-phase algorithm over a simple exploration planner. - D. K. Grady, M. Moll, and L. E. Kavraki, “Combining a POMDP Abstraction with Replanning to Solve Complex, Position-Dependent
Sensing Tasks,” in Proceedings of the AAAI Fall Symposium, Arlington, Virginia, 2013.
BibTeX
@inproceedings{grady-moll2013combining-pomdp-abstraction, title = {Combining a POMDP Abstraction with Replanning to Solve Complex, Position-Dependent Sensing Tasks}, author = {Grady, Devin K and Moll, Mark and Kavraki, Lydia E}, booktitle = {Proceedings of the AAAI Fall Symposium}, month = nov, year = {2013}, abstract = {The Partially-Observable Markov Decision Process (POMDP) is a general framework to determine reward-maximizing action policies under noisy action and sensing conditions. However, determining an optimal policy for POMDPs is often intractable for robotic tasks due to the PSPACE-complete nature of the computation required. Several recent solvers have been introduced that expand the size of problems that can be considered. Although these POMDP solvers can respect complex motion constraints in theory, we show that the computational cost does not provide a benefit in the eventual online execution, compared to our alternative approach that relies on a policy that ignores some of the motion constraints. We advocate using the POMDP framework where it is critical {\textendash} to find a policy that provides the optimal action given all past noisy sensor observations, while abstracting some of the motion constraints to reduce solution time. However, the actions of an abstract robot are generally not executable under its true motion constraints. The problem is addressed offline with a less-constrained POMDP, and navigation under the full system constraints is handled online with replanning. We empirically demonstrate that the policy generated using this abstracted motion model is faster to compute and achieves similar or higher reward than addressing the motion constraints for a car-like robot as used in our experiments directly in the POMDP.}, address = {Arlington, Virginia}, isbn = {978-1-57735-640-0}, keyword = {uncertainty}, publisher = {AAAI Press}, url = {https://www.aaai.org/ocs/index.php/FSS/FSS13/paper/view/7578} }DetailsAbstract
The Partially-Observable Markov Decision Process (POMDP) is a general framework to determine reward-maximizing action policies under noisy action and sensing conditions. However, determining an optimal policy for POMDPs is often intractable for robotic tasks due to the PSPACE-complete nature of the computation required. Several recent solvers have been introduced that expand the size of problems that can be considered. Although these POMDP solvers can respect complex motion constraints in theory, we show that the computational cost does not provide a benefit in the eventual online execution, compared to our alternative approach that relies on a policy that ignores some of the motion constraints. We advocate using the POMDP framework where it is critical – to find a policy that provides the optimal action given all past noisy sensor observations, while abstracting some of the motion constraints to reduce solution time. However, the actions of an abstract robot are generally not executable under its true motion constraints. The problem is addressed offline with a less-constrained POMDP, and navigation under the full system constraints is handled online with replanning. We empirically demonstrate that the policy generated using this abstracted motion model is faster to compute and achieves similar or higher reward than addressing the motion constraints for a car-like robot as used in our experiments directly in the POMDP. - R. Luna, I. A. Şucan, M. Moll, and L. E. Kavraki, “Anytime Solution Optimization for Sampling-Based Motion Planning,” in Proceedings of the IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 2013, pp. 5053–5059.
BibTeX
@inproceedings{luna-sucan2013anytime-solution-optimization, title = {Anytime Solution Optimization for Sampling-Based Motion Planning}, author = {Luna, Ryan and {\c S}ucan, Ioan A. and Moll, Mark and Kavraki, Lydia E}, booktitle = {Proceedings of the IEEE International Conference on Robotics and Automation}, month = may, year = {2013}, pages = {5053--5059}, doi = {10.1109/ICRA.2013.6631301}, abstract = {Recent work in sampling-based motion planning has yielded several different approaches for computing good quality paths in high degree of freedom systems: path shortcutting methods that attempt to shorten a single solution path by connecting non-consecutive configurations, a path hybridization technique that combines portions of two or more solutions to form a shorter path, and asymptotically optimal algorithms that converge to the shortest path over time. This paper presents an extensible meta-algorithm that incorporates a traditional sampling-based planning algorithm with offline path shorten- ing techniques to form an anytime algorithm which exhibits competitive solution lengths to the best known methods and optimizers. A series of experiments involving rigid motion and complex manipulation are performed as well as a comparison with asymptotically optimal methods which show the efficacy of the proposed scheme, particularly in high-dimensional spaces.}, address = {Karlsruhe, Germany}, keyword = {fundamentals of sampling-based motion planning} }DetailsAbstract
Recent work in sampling-based motion planning has yielded several different approaches for computing good quality paths in high degree of freedom systems: path shortcutting methods that attempt to shorten a single solution path by connecting non-consecutive configurations, a path hybridization technique that combines portions of two or more solutions to form a shorter path, and asymptotically optimal algorithms that converge to the shortest path over time. This paper presents an extensible meta-algorithm that incorporates a traditional sampling-based planning algorithm with offline path shorten- ing techniques to form an anytime algorithm which exhibits competitive solution lengths to the best known methods and optimizers. A series of experiments involving rigid motion and complex manipulation are performed as well as a comparison with asymptotically optimal methods which show the efficacy of the proposed scheme, particularly in high-dimensional spaces. - D. K. Grady, M. Moll, and L. E. Kavraki, “Automated Model Approximation for Robotic Navigation with POMDPs,” in Proceedings of the IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 2013, pp. 78–84.
BibTeX
@inproceedings{grady-moll2013automated-model-approximation, title = {Automated Model Approximation for Robotic Navigation with {POMDP}s}, author = {Grady, Devin K and Moll, Mark and Kavraki, Lydia E}, booktitle = {Proceedings of the IEEE International Conference on Robotics and Automation}, month = may, year = {2013}, pages = {78--84}, doi = {10.1109/ICRA.2013.6630559}, abstract = {Partially-Observable Markov Decision Processes (POMDPs) are a problem class with significant applicability to robotics when considering the uncertainty present in the real world, however, they quickly become intractable for large state and action spaces. A method to create a less complex but accurate action model approximation is proposed and evaluated using a state-of-the-art POMDP solver. We apply this general and powerful formulation to a robotic navigation task under state and sensing uncertainty. Results show that this method can provide a useful action model that yields a policy with similar overall expected reward compared to the true action model, often with significant computational savings. In some cases, our reduced complexity model can solve problems where the true model is too complex to find a policy that accomplishes the task. We conclude that this technique of building problem-dependent approximations can provide significant computational advantages and can help expand the complexity of problems that can be considered using current POMDP techniques.}, address = {Karlsruhe, Germany}, keyword = {uncertainty}, publisher = {IEEE} }DetailsAbstract
Partially-Observable Markov Decision Processes (POMDPs) are a problem class with significant applicability to robotics when considering the uncertainty present in the real world, however, they quickly become intractable for large state and action spaces. A method to create a less complex but accurate action model approximation is proposed and evaluated using a state-of-the-art POMDP solver. We apply this general and powerful formulation to a robotic navigation task under state and sensing uncertainty. Results show that this method can provide a useful action model that yields a policy with similar overall expected reward compared to the true action model, often with significant computational savings. In some cases, our reduced complexity model can solve problems where the true model is too complex to find a policy that accomplishes the task. We conclude that this technique of building problem-dependent approximations can provide significant computational advantages and can help expand the complexity of problems that can be considered using current POMDP techniques. - M. R. Maly, M. Lahijanian, L. E. Kavraki, H. Kress-Gazit, and M. Y. Vardi, “Iterative Temporal Motion Planning for Hybrid Systems in Partially Unknown
Environments,” in ACM International Conference on Hybrid Systems: Computation and Control (HSCC), Philadelphia, PA, USA, 2013, pp. 353–362.
BibTeX
@inproceedings{maly-lahijanian2013iterative-temporal-motion, title = {Iterative Temporal Motion Planning for Hybrid Systems in Partially Unknown Environments}, author = {Maly, MR and Lahijanian, M and Kavraki, Lydia E and Kress-Gazit, H. and Vardi, Moshe Y.}, booktitle = {ACM International Conference on Hybrid Systems: Computation and Control (HSCC)}, month = apr, year = {2013}, pages = {353--362}, doi = {10.1145/2461328.2461380}, abstract = {This paper considers the problem of motion planning for a hybrid robotic system with complex and nonlinear dynamics in a partially unknown environment given a temporal logic specification. We employ a multi-layered synergistic framework that can deal with general robot dynamics and combine it with an iterative planning strategy. Our work allows us to deal with the unknown environmental restrictions only when they are discovered and without the need to repeat the computation that is related to the temporal logic specification. In addition, we define a metric for satisfaction of a specification. We use this metric to plan a trajectory that satisfies the specification as closely as possible in cases in which the discovered constraint in the environment renders the specification unsatisfiable. We demonstrate the efficacy of our framework on a simulation of a hybrid second-order car-like robot moving in an office environment with unknown obstacles. The results show that our framework is successful in generating a trajectory whose satisfaction measure of the specification is optimal. They also show that, when new obstacles are discovered, the reinitialization of our framework is computationally inexpensive.}, address = {Philadelphia, PA, USA}, keyword = {planning from high-level specifications}, publisher = {ACM} }DetailsAbstract
This paper considers the problem of motion planning for a hybrid robotic system with complex and nonlinear dynamics in a partially unknown environment given a temporal logic specification. We employ a multi-layered synergistic framework that can deal with general robot dynamics and combine it with an iterative planning strategy. Our work allows us to deal with the unknown environmental restrictions only when they are discovered and without the need to repeat the computation that is related to the temporal logic specification. In addition, we define a metric for satisfaction of a specification. We use this metric to plan a trajectory that satisfies the specification as closely as possible in cases in which the discovered constraint in the environment renders the specification unsatisfiable. We demonstrate the efficacy of our framework on a simulation of a hybrid second-order car-like robot moving in an office environment with unknown obstacles. The results show that our framework is successful in generating a trajectory whose satisfaction measure of the specification is optimal. They also show that, when new obstacles are discovered, the reinitialization of our framework is computationally inexpensive. - E. Plaku, L. E. Kavraki, and M. Y. Vardi, “Falsification of LTL safety properties in hybrid systems,” International Journal on Software Tools for Technology Transfer (STTT), vol. 15, no. 4, pp. 305–320, 2013.
DetailsBibTeX
@article{plaku-kavraki2013falsification-of-ltl, title = {Falsification of {LTL} safety properties in hybrid systems}, author = {Plaku, E. and Kavraki, Lydia E and Vardi, Moshe Y.}, journal = {International Journal on Software Tools for Technology Transfer (STTT)}, year = {2013}, volume = {15}, number = {4}, pages = {305--320}, doi = {10.1007/s10009-012-0233-2}, issn = {1433-2779}, keyword = {planning from high-level specifications}, publisher = {Springer Berlin / Heidelberg} } - B. Gipson, M. Moll, and L. E. Kavraki, “Resolution Independent Density Estimation for Motion Planning in High-Dimensional
Spaces,” in IEEE International Conference on Robotics and Automation, 2013, pp. 2429–2435.
BibTeX
@inproceedings{gipson-moll2013resolution-independent-density, title = {Resolution Independent Density Estimation for Motion Planning in High-Dimensional Spaces}, author = {Gipson, B and Moll, Mark and Kavraki, Lydia E}, booktitle = {IEEE International Conference on Robotics and Automation}, year = {2013}, pages = {2429--2435}, doi = {10.1109/ICRA.2013.6630908}, abstract = {This paper presents a new motion planner, Search Tree with Resolution Independent Density Estimation (STRIDE), designed for rapid exploration and path planning in high-dimensional systems (greater than 10). A Geometric Near- neighbor Access Tree (GNAT) is maintained to estimate the sampling density of the configuration space, allowing an implicit, resolution-independent, Voronoi partitioning to provide sampling density estimates, naturally guiding the planner towards unexplored regions of the configuration space. This planner is capable of rapid exploration in the full dimension of the configuration space and, given that a GNAT requires only a valid distance metric, STRIDE is largely parameter-free. Extensive experimental results demonstrate significant dimension- dependent performance improvements over alternative state-of-the-art planners. In particular, high-dimensional systems where the free space is mostly defined by narrow passages were found to yield the greatest performance improvements. Experimental results are shown for both a classical 6-dimensional problem and those for which the dimension incrementally varies from 3 to 27.}, keyword = {fundamentals of sampling-based motion planning} }DetailsAbstract
This paper presents a new motion planner, Search Tree with Resolution Independent Density Estimation (STRIDE), designed for rapid exploration and path planning in high-dimensional systems (greater than 10). A Geometric Near- neighbor Access Tree (GNAT) is maintained to estimate the sampling density of the configuration space, allowing an implicit, resolution-independent, Voronoi partitioning to provide sampling density estimates, naturally guiding the planner towards unexplored regions of the configuration space. This planner is capable of rapid exploration in the full dimension of the configuration space and, given that a GNAT requires only a valid distance metric, STRIDE is largely parameter-free. Extensive experimental results demonstrate significant dimension- dependent performance improvements over alternative state-of-the-art planners. In particular, high-dimensional systems where the free space is mostly defined by narrow passages were found to yield the greatest performance improvements. Experimental results are shown for both a classical 6-dimensional problem and those for which the dimension incrementally varies from 3 to 27. - D. K. Grady, M. Moll, C. Hegde, A. C. Sankaranarayanan, R. G. Baraniuk, and L. E. Kavraki, “Multi-Robot Target Verification with Reachability Constraints,” in IEEE International Symposium on Safety, Security, and Rescue Robotics, College Station, TX, 2012, pp. 1–6.
BibTeX
@inproceedings{grady-moll2012multi-robot-target-verification, title = {Multi-Robot Target Verification with Reachability Constraints}, author = {Grady, Devin K and Moll, Mark and Hegde, Chinmay and Sankaranarayanan, Aswin C. and Baraniuk, Richard G. and Kavraki, Lydia E}, booktitle = {IEEE International Symposium on Safety, Security, and Rescue Robotics}, month = nov, year = {2012}, pages = {1--6}, doi = {10.1109/SSRR.2012.6523873}, abstract = {This paper studies a core problem in multi-objective mission planning for robots governed by differential constraints. The problem considered is the following. A car-like robot computes a plan to move from a start configuration to a goal region. The robot is equipped with a sensor that can alert it if an anomaly appears within some range while the robot is moving. In that case, the robot tries to deviate from its computed path and gather more information about the target without incurring considerable delays in fulfilling its primary mission, which is to move to its final destination. This problem is important in, e.g., surveillance, where inspection of possible threats needs to be balanced with completing a nominal route. The paper presents a simple and intuitive framework to study the trade-offs present in the above problem. Our work utilizes a state-of-the-art sampling-based planner, which employs both a high-level discrete guide and low-level planning. We show that modifications to the distance function used by the planner and to the weights that the planner employs to compute the high-level guide can help the robot react online to new secondary objectives that were unknown at the outset of the mission. The modifications are computed using information obtained from a conventional camera model. We find that for small percentage increases in path length, the robot can achieve significant gains in information about an unexpected target.}, address = {College Station, TX}, isbn = {978-1-4799-0164-7}, keyword = {planning from high-level specifications, uncertainty}, publisher = {IEEE} }DetailsAbstract
This paper studies a core problem in multi-objective mission planning for robots governed by differential constraints. The problem considered is the following. A car-like robot computes a plan to move from a start configuration to a goal region. The robot is equipped with a sensor that can alert it if an anomaly appears within some range while the robot is moving. In that case, the robot tries to deviate from its computed path and gather more information about the target without incurring considerable delays in fulfilling its primary mission, which is to move to its final destination. This problem is important in, e.g., surveillance, where inspection of possible threats needs to be balanced with completing a nominal route. The paper presents a simple and intuitive framework to study the trade-offs present in the above problem. Our work utilizes a state-of-the-art sampling-based planner, which employs both a high-level discrete guide and low-level planning. We show that modifications to the distance function used by the planner and to the weights that the planner employs to compute the high-level guide can help the robot react online to new secondary objectives that were unknown at the outset of the mission. The modifications are computed using information obtained from a conventional camera model. We find that for small percentage increases in path length, the robot can achieve significant gains in information about an unexpected target. - D. K. Grady, M. Moll, C. Hegde, A. C. Sankaranarayanan, R. G. Baraniuk, and L. E. Kavraki, “Multi-Objective Sensor-Based Replanning for a Car-Like Robot,” in IEEE International Symposium on Safety, Security, and Rescue Robotics, College Station, TX, 2012, pp. 1–6.
BibTeX
@inproceedings{grady-moll2012multi-objective-sensor-based-replanning, title = {Multi-Objective Sensor-Based Replanning for a Car-Like Robot}, author = {Grady, Devin K and Moll, Mark and Hegde, Chinmay and Sankaranarayanan, Aswin C. and Baraniuk, Richard G. and Kavraki, Lydia E}, booktitle = {IEEE International Symposium on Safety, Security, and Rescue Robotics}, month = nov, year = {2012}, pages = {1--6}, doi = {10.1109/SSRR.2012.6523898}, abstract = {In search and rescue applications it is important that mobile ground robots can verify whether a potential target/victim is indeed a target of interest. This paper describes a novel approach to multi-robot target verification of multiple static objects. Suppose a team of multiple mobile ground robots are operating in a partially known environment with knowledge of possible target locations and obstacles. The ground robots{\textquoteright} goal is to (a) collectively classify the targets (or build models of them) by identifying good viewpoints to sense the targets, while (b) coordinating their actions to execute the mission and always be safe by avoiding obstacles and each other. As opposed to a traditional next-best-view (NBV) algorithm that generates a single good view, we characterize the informativeness of all potential views. We propose a measure for the informativeness of a view that exploits the geometric structure of the pose manifold. This information is encoded in a cost map that guides a multi-robot motion planning algorithm towards views that are both reachable and informative. Finally, we account for differential constraints in the robots{\textquoteright} motion that prevent unrealistic scenarios such as the robots stopping or turning instantaneously. A range of simulations indicates that our approach outperforms current approaches and demonstrates the advantages of predictive sensing and accounting for reachability constraints.}, address = {College Station, TX}, isbn = {978-1-4799-0164-7}, keyword = {planning from high-level specifications, uncertainty}, publisher = {IEEE} }DetailsAbstract
In search and rescue applications it is important that mobile ground robots can verify whether a potential target/victim is indeed a target of interest. This paper describes a novel approach to multi-robot target verification of multiple static objects. Suppose a team of multiple mobile ground robots are operating in a partially known environment with knowledge of possible target locations and obstacles. The ground robots’ goal is to (a) collectively classify the targets (or build models of them) by identifying good viewpoints to sense the targets, while (b) coordinating their actions to execute the mission and always be safe by avoiding obstacles and each other. As opposed to a traditional next-best-view (NBV) algorithm that generates a single good view, we characterize the informativeness of all potential views. We propose a measure for the informativeness of a view that exploits the geometric structure of the pose manifold. This information is encoded in a cost map that guides a multi-robot motion planning algorithm towards views that are both reachable and informative. Finally, we account for differential constraints in the robots’ motion that prevent unrealistic scenarios such as the robots stopping or turning instantaneously. A range of simulations indicates that our approach outperforms current approaches and demonstrates the advantages of predictive sensing and accounting for reachability constraints. - M. R. Maly and L. E. Kavraki, “Low-Dimensional Projections for SyCLoP,” in IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura, Algarve, Portugal, 2012, pp. 420–425.
BibTeX
@inproceedings{maly-kavraki2012low-dimensional-projections-for, title = {Low-Dimensional Projections for SyCLoP}, author = {Maly, MR and Kavraki, Lydia E}, booktitle = {IEEE/RSJ International Conference on Intelligent Robots and Systems}, month = oct, year = {2012}, pages = {420--425}, doi = {10.1109/IROS.2012.6386202}, abstract = {This paper presents an extension to SyCLoP, a multilayered motion planning framework that has been shown to successfully solve high-dimensional problems with differen- tial constraints. SyCLoP combines traditional sampling-based planning with a high-level decomposition of the workspace through which it attempts to guide a low-level tree of motions. We investigate a generalization of SyCLoP in which the high- level decomposition is defined over a given low-dimensional projected subspace of the state space. We begin with a manually-chosen projection to demonstrate that projections other than the workspace can potentially work well. We then evaluate SyCLoP{\textquoteright}s performance with random projections and projections determined from linear dimensionality reduction over elements of the state space, for which the results are mixed. As we will see, finding a useful projection is a difficult problem, and we conclude this paper by discussing the merits and drawbacks of various types of projections.}, address = {Vilamoura, Algarve, Portugal}, keyword = {planning from high-level specifications} }DetailsAbstract
This paper presents an extension to SyCLoP, a multilayered motion planning framework that has been shown to successfully solve high-dimensional problems with differen- tial constraints. SyCLoP combines traditional sampling-based planning with a high-level decomposition of the workspace through which it attempts to guide a low-level tree of motions. We investigate a generalization of SyCLoP in which the high- level decomposition is defined over a given low-dimensional projected subspace of the state space. We begin with a manually-chosen projection to demonstrate that projections other than the workspace can potentially work well. We then evaluate SyCLoP’s performance with random projections and projections determined from linear dimensionality reduction over elements of the state space, for which the results are mixed. As we will see, finding a useful projection is a difficult problem, and we conclude this paper by discussing the merits and drawbacks of various types of projections. - I. A. Sucan and L. E. Kavraki, “Accounting for Uncertainty in Simultaneous Task and Motion Planning Using Task Motion
Multigraphs,” in IEEE International Conference on Robotics and Automation, St. Paul, 2012, pp. 4822–4828.
BibTeX
@inproceedings{sucan-kavraki2012accounting-for-uncertainty, title = {Accounting for Uncertainty in Simultaneous Task and Motion Planning Using Task Motion Multigraphs}, author = {Sucan, Ioan Alexandru and Kavraki, Lydia E}, booktitle = {IEEE International Conference on Robotics and Automation}, month = may, year = {2012}, pages = {4822--4828}, doi = {10.1109/ICRA.2012.6224885}, abstract = {This paper describes an algorithm that considers uncertainty while solving the simultaneous task and motion planning (STAMP) problem. Information about uncertainty is transferred to the task planning level from the motion planning level using the concept of a task motion multigraph (TMM). TMMs were introduced in previous work to improve the efficiency of solving the STAMP problem for mobile manipulators. In this work, Markov Decision Processes are used in conjunction with TMMs to select sequences of actions that solve the STAMP problem such that the resulting solutions have higher probability of feasibility. Experimental evaluation indicates significantly improved probability of feasibility for solutions to the STAMP problem, compared to algorithms that ignore uncertainty information when selecting possible sequences of actions. At the same time, the efficiency due to TMMs is largely maintained.}, address = {St. Paul}, keyword = {planning from high-level specifications, uncertainty} }DetailsAbstract
This paper describes an algorithm that considers uncertainty while solving the simultaneous task and motion planning (STAMP) problem. Information about uncertainty is transferred to the task planning level from the motion planning level using the concept of a task motion multigraph (TMM). TMMs were introduced in previous work to improve the efficiency of solving the STAMP problem for mobile manipulators. In this work, Markov Decision Processes are used in conjunction with TMMs to select sequences of actions that solve the STAMP problem such that the resulting solutions have higher probability of feasibility. Experimental evaluation indicates significantly improved probability of feasibility for solutions to the STAMP problem, compared to algorithms that ignore uncertainty information when selecting possible sequences of actions. At the same time, the efficiency due to TMMs is largely maintained. - K. E. Bekris, D. K. Grady, M. Moll, and L. E. Kavraki, “Safe Distributed Motion Coordination for Second-Order Systems With Different Planning
Cycles,” International Journal of Robotics Research, vol. 31, no. 2, pp. 129–150, Feb. 2012.
BibTeX
@article{bekris-grady2012safe-distributed-motion, title = {Safe Distributed Motion Coordination for Second-Order Systems With Different Planning Cycles}, author = {Bekris, Kostas E. and Grady, Devin K and Moll, Mark and Kavraki, Lydia E}, journal = {International Journal of Robotics Research}, month = feb, year = {2012}, volume = {31}, number = {2}, pages = {129--150}, doi = {10.1177/0278364911430420}, abstract = {When multiple robots operate in the same environment, it is desirable for scalability purposes to coordinate their motion in a distributed fashion while providing guarantees about their safety. If the robots have to respect second-order dynamics, this becomes a challenging problem, even for static environments. This work presents a replanning framework where each robot computes partial plans during each cycle, while executing a previously computed trajectory. Each robot communicates with its neighbors to select a trajectory that is safe over an infinite time horizon. The proposed approach does not require synchronization and allows the robots to dynamically change their cycles over time. This paper proves that the proposed motion coordination algorithm guarantees safety under this general setting. This framework is not specific to the underlying robot dynamics, as it can be used with a variety of dynamical systems, nor to the planning or control algorithm used to generate the robot trajectories. The performance of the approach is evaluated using a distributed multi-robot simulator on a computing cluster, where the simulated robots are forced to communicate by exchanging messages. The simulation results confirm the safety of the algorithm in various environments with up to 32 robots governed by second-order dynamics.}, chapter = {129}, keyword = {kinodynamic systems} }DetailsAbstract
When multiple robots operate in the same environment, it is desirable for scalability purposes to coordinate their motion in a distributed fashion while providing guarantees about their safety. If the robots have to respect second-order dynamics, this becomes a challenging problem, even for static environments. This work presents a replanning framework where each robot computes partial plans during each cycle, while executing a previously computed trajectory. Each robot communicates with its neighbors to select a trajectory that is safe over an infinite time horizon. The proposed approach does not require synchronization and allows the robots to dynamically change their cycles over time. This paper proves that the proposed motion coordination algorithm guarantees safety under this general setting. This framework is not specific to the underlying robot dynamics, as it can be used with a variety of dynamical systems, nor to the planning or control algorithm used to generate the robot trajectories. The performance of the approach is evaluated using a distributed multi-robot simulator on a computing cluster, where the simulated robots are forced to communicate by exchanging messages. The simulation results confirm the safety of the algorithm in various environments with up to 32 robots governed by second-order dynamics. - A. Bhatia, M. R. Maly, L. E. Kavraki, and M. Y. Vardi, “Motion Planning with Complex Goals,” Robotics Automation Magazine, IEEE, vol. 18, no. 3, pp. 55–64, Sep. 2011.
BibTeX
@article{bhatia-maly2011motion-planning-with, title = {Motion Planning with Complex Goals}, author = {Bhatia, Amit and Maly, MR and Kavraki, Lydia E and Vardi, Moshe Y.}, journal = {Robotics Automation Magazine, IEEE}, month = sep, year = {2011}, volume = {18}, number = {3}, pages = {55--64}, doi = {10.1109/MRA.2011.942115}, abstract = {This article describes approach for solving motion planning problems for mobile robots involving temporal goals. Traditional motion planning for mobile robotic systems involves the construction of a motion plan that takes the system from an initial state to a set of goal states while avoiding collisions with obstacles at all times. The motion plan is also required to respect the dynamics of the system that are typically described by a set of differential equations. A wide variety of techniques have been pro posed over the last two decades to solve such problems [1], [2].}, issn = {1070-9932}, keyword = {planning from high-level specifications} }DetailsAbstract
This article describes approach for solving motion planning problems for mobile robots involving temporal goals. Traditional motion planning for mobile robotic systems involves the construction of a motion plan that takes the system from an initial state to a set of goal states while avoiding collisions with obstacles at all times. The motion plan is also required to respect the dynamics of the system that are typically described by a set of differential equations. A wide variety of techniques have been pro posed over the last two decades to solve such problems [1], [2]. - I. A. Sucan and L. E. Kavraki, “On the Advantages of Using Task Motion Multigraphs for Efficient Mobile Manipulation,” in IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, 2011, pp. 4621–4626.
DetailsBibTeX
@inproceedings{sucan-kavraki2011on-advantages-of, title = {On the Advantages of Using Task Motion Multigraphs for Efficient Mobile Manipulation}, author = {Sucan, Ioan Alexandru and Kavraki, Lydia E}, booktitle = {IEEE/RSJ International Conference on Intelligent Robots and Systems}, year = {2011}, pages = {4621--4626}, doi = {10.1109/IROS.2011.6048260}, address = {San Francisco, CA}, keyword = {planning from high-level specifications} } - I. A. Sucan and L. E. Kavraki, “Mobile Manipulation: Encoding Motion Planning Options Using Task Motion Multigraphs,” in IEEE International Conference on Robotics and Automation, Shanghai, China, 2011, pp. 5492–5498.
DetailsBibTeX
@inproceedings{sucan-kavraki2011mobile-manipulation-encoding, title = {Mobile Manipulation: Encoding Motion Planning Options Using Task Motion Multigraphs}, author = {Sucan, Ioan Alexandru and Kavraki, Lydia E}, booktitle = {IEEE International Conference on Robotics and Automation}, year = {2011}, pages = {5492--5498}, doi = {10.1109/ICRA.2011.5980212}, address = {Shanghai, China}, keyword = {planning from high-level specifications} }